[Algorithm] 위상

토폴로지 정렬?

위상 정렬은 순차적으로 정렬된 작업을 수행할 때 순서를 결정하는 데 사용되는 알고리즘입니다. 방향성 비순환 그래프(DAG)에서 정점을 선형적으로 정렬합니다.하는 것이다

예를 들어 실생활에서,

인터넷을 검색하려면 다음 순서대로 진행해야 합니다.

컴퓨터 켜기 -> 브라우저 켜기 -> 검색 엔진 포털 불러오기 -> 검색

위의 순서가 바뀌면 검색이 되지 않습니다.

위상 정렬에서 모든 모서리(u,v)는 정점 u가 정점 v에 선행하는 순서로 정렬됩니다.

그래프 DAG가 아닌 그래프에서는 토폴로지 정렬이 불가능합니다.하다.

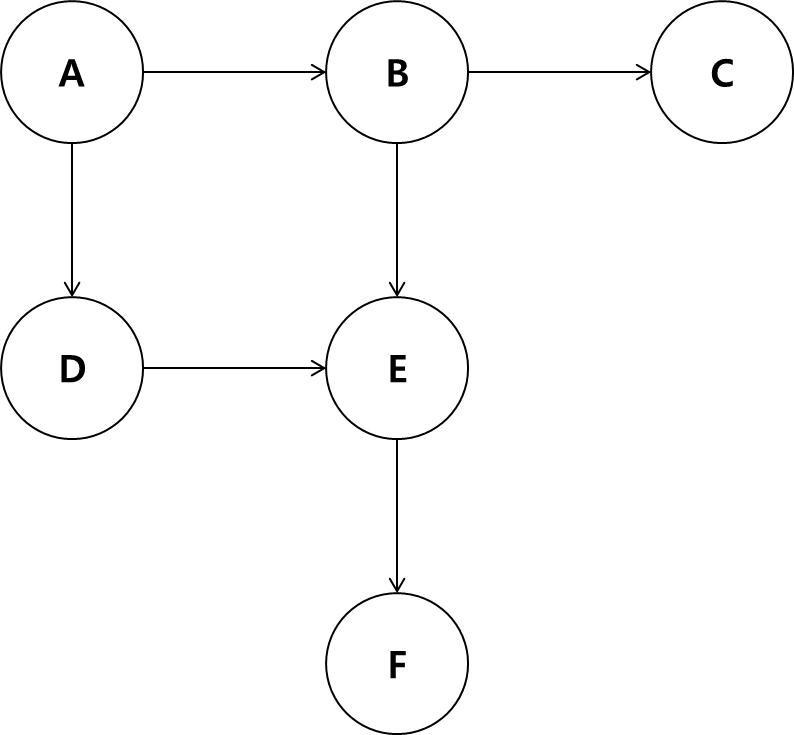
E를 실행하려면 B와 D를 모두 실행해야 합니다.

방향성 비순환 그래프(DAG)?

방향성 비순환 그래프(DAG)~이다 주기가 없는 유방향 그래프오전.

DAG는 주로 이벤트 간의 우선 순위를 나타내는 데 사용됩니다.

화신

토폴로지 정렬은 BFS와 DFS의 두 가지 방법으로 구현할 수 있습니다.

BFS로 구현

1. 모든 정점의 차수(inDegree)를 설정합니다.
2. 차수가 0인 정점을 방문한 것으로 표시하고 해당 정점을 대기열에 추가합니다.
3. 요소를 대기열에서 빼고 인접한 방문하지 않은 꼭지점의 In 차수를 하나씩 줄입니다.
4. 인도가 0에 도달하는 정점이 대기열에 추가됩니다.
5. 대기열이 비워질 때까지 2~4단계를 반복합니다.

import java.util.*;

public class TopologicalSort {

    private static int()() graph = {{},
            {2, 4},
            {3, 5},
            {},
            {5},
            {6},
            {}};
    private static int() inDegree;
    public static void main(String() args) {
        inDegree = new int(graph.length);

        setInDegree();
        search(1);
    }

    public static void setInDegree() {
        for (int i = 1; i < graph.length; i++) {
            for (int next : graph(i)) {
                inDegree(next)++;
            }
        }
    }

    public static void search(int start) {
        Deque<Integer> dq = new ArrayDeque<>();
        dq.offer(start);

        while (!dq.isEmpty()) {
            int cur = dq.poll();
            System.out.print(cur + " ");

            for (int next : graph(cur)) {
                if (inDegree(next) == 0) {
                    continue;
                }

                if (--inDegree(next) == 0) {
                    dq.offer(next);
                }
            }
        }
    }
}